A palavra Trigonometria tem origem grega: TRI (três), GONO (ângulo) e METRIEN (medida). Etimologicamente, significa medida de triângulos. Trata-se, assim, do estudo das relações entre os lados e os ângulos de um triângulo.
Apesar dos egípcios e dos babilónios terem utilizado as relações existentes entre lados e ângulos dos triângulos, para resolver problemas, foi a atracção pelo movimento dos astros que impulsionou a evolução da Trigonometria. Daí que, historicamente a Trigonometria apareça muito cedo associada à Astronomia.

As medições e os resultados dos cálculos feitos pelos astrónomos eram registados
Surgiu então, na segunda metade do século dois a.C., um marco na história da trigonometria: Hiparco de Nicéia (180-
Hiparco construiu o que foi presumivelmente a primeira tabela trigonométrica com os valores das cordas de ângulos de 0° a 180°.
Assim, Hiparco representou um grande avanço na Astronomia e por isso recebeu o título de “Pai da Trigonometria”.

Outra tábua, também de cordas, mas mais completa foi construída por Ptolomeu (séc. II). Esta já possuía cordas para ângulos crescentes, desde 0º até 180º, em intervalos de 1/2 graus. O raio usado era diferente do de Hiparcus, sendo também fixo e muito grande. Note-se que o facto de usar um raio muito grande diminui o uso de fracções.
Foi Ptolomeu (séc. II) quem influenciou o desenvolvimento da Trigonometria, durante muitos séculos. A sua obra Almagesto contém uma tabela de cordas correspondentes a diversos ângulos, por ordem crescente e em função da metade do ângulo, que é equivalente a uma tabela de senos, bem como uma série de proposições da actual disciplina. No Almagesto reuniu os conhecimentos existentes na época sobre Astronomia e Trigonometria e a que os árabes tiveram acesso. Estes introduziram os conhecimentos de Trigonometria para a Europa através de Espanha.
A relação da Astronomia com a Trigonometria fez com que esta se desenvolvesse aplicada a triângulos curvos de lados curvilíneos que se formam sobre a superfície esférica. Assim, a Trigonometria Esférica desenvolveu-se anteriormente à Trigonometria Plana, o que se deveu ao facto de a Trigonometria Esférica ser muito utilizada nos cálculos astronómicos e na navegação, sendo sistematizada por árabes e hindus até meados do séc. XIII. A contribuição destes foi bastante grande, tendo calculado tabelas de senos para intervalos com variação de
O recurso constante ao círculo trigonométrico e a aplicação da Trigonometria à resolução de problemas algébricos é feita por Viète– séc. XVI – que estabeleceu também alguns resultados importantes.
Contudo, foi Euler (séc. XVIII) que, ao usar invariavelmente o círculo de raio um, introduziu o conceito de seno, de co-seno e de tangente como números, bem como as notações actualmente utilizadas.
O primeiro vestígio do tratamento funcional da Trigonometria surgiu em 1635, quando Roberval fez o primeiro esboço de uma curva do seno. Mas, a ligação da Trigonometria à Análise só é feita por Fourier (séc. XIX), como consequência do estudo dos movimentos periódicos por ele efectuado.
As funções trigonométricas como o seno, o coseno e a tangente, relacionam medidas de ângulos, a medidas de segmentos de recta a eles associados.
Actualmente a trigonometria não se limita a estudar os triângulos. Encontramos aplicações na mecânica, electricidade, acústica, música, astronomia, engenharia, medicina, enfim, em muitos outros campos da actividade humana. Essas aplicações envolvem conceitos que dificilmente lembram os triângulos que deram origem à trigonometria:
Há métodos actuais de análise em medicina, onde são enviadas ondas ao coração, de forma que efectuem interacções selectivas com os tecidos a observar
Geodésia: estudo da forma e dimensão da Terra
Método do momento eléctrico para cálculo de linhas de transporte de energia eléctrica: permite calcular com grande sensibilidade a potência de transporte de linhas, as perdas e a distância a que ela poderá ser transportada
Estudo da intensidade luminosa: calcula-se a intensidade luminosa irradiada por uma fonte luminosa para uma determinada direcção
Instrumentos de medidas de ângulos: topografia, ciência náutica e cartografia
- Numa pesquisa realizada em 1997, com engenheiros que actuam em empresas de grande porte da região da Serra Gaúcha, foi constatado que a trigonometria é o conceito de matemática básica mais utilizado por eles no seu cotidiano.
Fonte: http://migre.me/5uwsU
.jpg)
.jpg)


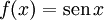
![\operatorname{Im} = [-1, 1]](http://upload.wikimedia.org/math/8/9/e/89efdaea105b3963eb51d030df18585f.png)


![\operatorname{Im} = \left]-\infty, \infty \right[](http://upload.wikimedia.org/math/a/4/0/a40542781d0533e14250e9dca474615b.png)






